RL-based LLMs - RLPrompt
In this post, I am going to review the RLPrompt paper. The combination of prompt engineering and reinforcement learning is the main interesting novelty of this paper.
RLPrompt: Optimizing Discrete Text Prompts with Reinforcement Learning
This paper proposed an RL-based approach for optimizing the discrete prompts. In this regard, they consider the language model as a black-box. So, to reach a reasonable performance for different downstream tasks, their focus is only on optimzing the input by choosing the best possible prompt. In addition their focus is on discrete prompts, optimizing which is much harder than soft prompts.
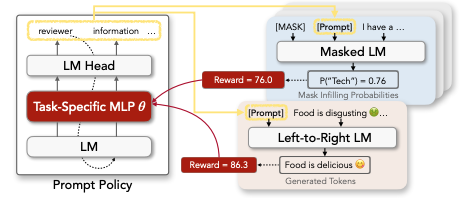
Generally, RLPrompt is a Multi-Layer Perceptron (MLP)–represented by \(\pi\)–which is same as the policy concept in RL. Let us say that \(\theta\) is the weights and parameter-set for \(\pi\). Then, we can use the notation of \(\pi_{\theta}\) to denote the MLP and its parameters. So, for each downstream task, \(\pi_{\theta}\) is first trained to find the optimal set of prompts. From then, the optimal prompts can be used for that specific downstream task. But the question is that how such MLP should be trained in order to find the optimal prompts per task?
Let us say that we are going to train \(\pi_{\theta}\) for task \(D\) (e.g., a classification task), then the training procedure is as follows:
-
First, we need to get the embedding of input \(x\). So, we can use an embedding model for encoding the input sentence. This embedding model can be any language model, such as BERT, DistillBERT, RoBERTa, etc.
-
Input \(x\) is passed to \(\pi_{\theta}\) and the prompt set \(z\) is returned. To be more specific, \(\pi_{\theta}\) returns a token for each round. So, for generating a prompt with \(T\) tokens, it should be called for \(T\) times. If we want to have a prompt of size \(T\), then we need to get the tokens corresponding to the top \(T\) highest probabilities. (\(z = [z_1, ..., z_T]\))
-
The concatenation of prompt \(z\) and the input \(x\) are passed to the langugage model which is used for downstream task \(D\). This language model is represetend by \(LM\), and its output is denoted by \(y_{LM}(z, x)\). The performance of the LM for task \(D\) is represented as \(R\). \(R\) is a function which takes the output of the langugae model as input and returns the score (how well is the output)–\(score = R(y_{LM}(z, x))\). For example, for the classification task, \(R\) is the how frequent the model can predict the gold label. Moreover, the authors mention that for having a stable MLP the score value should be normalized!
-
According to the \(score\) value computed in the previous step, \(\pi_{\theta}\) is trained and \(\theta\) is updated.
-
The training process is continued for some while. After that, the output trained \(\pi_{\theta}\) is called \(\hat{z}\). In general, the problem can be formulated as finding \(\theta\) such that: \(max_{\theta} R(y_{LM}(\hat{z}, x)), \hat{z} \sim \prod_{t=1}^T\pi_{\theta}(z_t|Z_{<t})\)
The whole procedure is depited in the following figure:
The main advantages of the paper are that:
- They have considered an offline RL approach for finding the optimal prompt for different downstream tasks, considering having a freezed and black-box language model.
- They represent that the optimal prompt which is found for a specific task and based on a specific language model can be transfered to other language models as well!
- The output of MLP is usually an ungrammatical gibberish text. This proves that usually the prompts which work the best for LMs is way too different from what humans create!
- My Comment: One of the main highlights of the paper is that they are using discrete prompts. However, after MLP, there is no component to check whether the generate prompt exists in the vocabulary \(V\) or not. This point and also the fact that the decoded prompts are usually gibberish leads to the result that the generated prompt is not discrete anymore. To me, it sounds like it is a soft and continous prompt. So, I don’t understand why they are insisting that their approach is based on discrete prompts.
Here are some more articles relevant to this one: