Paper Review - Week 2
Several interesting papers are published in this week in NLP. Here is a list of them:
Mixtral of Experts
Introduction
In the cutting-edge realm of AI and natural language processing, the Mixtral 8x7B emerges as a groundbreaking development, introducing a new paradigm in transformer-based language models. This innovative model, built on the Sparse Mixture of Experts (SMoE) framework, evolves from the established Mistral 7B model, with a critical advancement in its architecture. Mixtral is distinguished by its unique design, integrating 8 feedforward blocks, or ‘experts’, into each transformer layer. This structure enables a dynamic selection process where each token, at every layer, is processed by two specifically chosen experts, allowing the model to efficiently utilize its immense 47B parameter capacity while actively employing only 13B parameters during inference. By using such transformative approach, Mixtral shows exceptional performance in benchmarks spanning mathematics, code generation, and multilingual tasks. The paper also introduces the Mixtral 8x7B – Instruct, a variant fine-tuned for instruction-following, which notably outperforms leading models in human-centric evaluations.
Research Gap
The Mixtral 8x7B paper addresses a critical research gap in the field of transformer-based language models, focusing on improving inference efficiency without sacrificing performance. Traditional large-scale models like GPT-3.5 and Llama 2 70B, while powerful, often struggle with the balance between their extensive parameter counts and the need for efficient inference. These models typically require substantial computational resources for processing inputs, making them less efficient in scenarios that demand quick response times or involve large batch sizes.
Mixtral 8x7B confronts this challenge by integrating a Sparse Mixture of Experts (SMoE) framework into its transformer architecture. This innovative approach allows the model to selectively utilize its parameters during inference, activating only a fraction of the available experts for each token. As a result, Mixtral dramatically reduces the active parameter count during inference, leading to faster response times and improved throughput. This selective expert activation does not compromise the model’s ability to handle complex tasks, such as mathematics, code generation, and multilingual processing.
Solution: Mixtral
The Mixtral 8x7B model introduces a transformative approach to transformer-based architecture, addressing the inefficiencies of previous models. As depicted in Figure 1, the traditional transformer employs a standard sequence of operations, starting from input embedding, followed by positional encoding, multi-head attention, and a feed-forward network, with layer normalization steps in between.
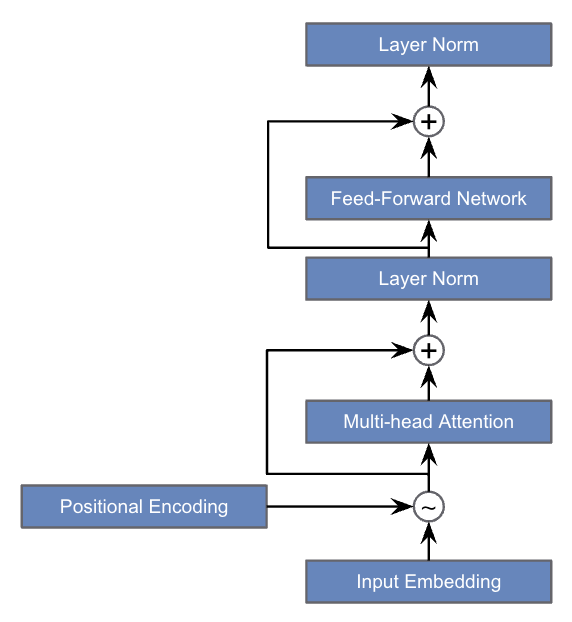
In contrast, the Mixtral model, shown in Figure 2, redefines this architecture by integrating a routing mechanism within the transformer layers. Each layer in Mixtral consists of 8 FFN, termed experts. Unlike the uniform processing in traditional transformers, Mixtral employs a router network that selects two of these experts at each layer to process the input token. This selective processing is a key differentiator, enabling Mixtral to leverage a large number of parameters while maintaining computational efficiency during inference.
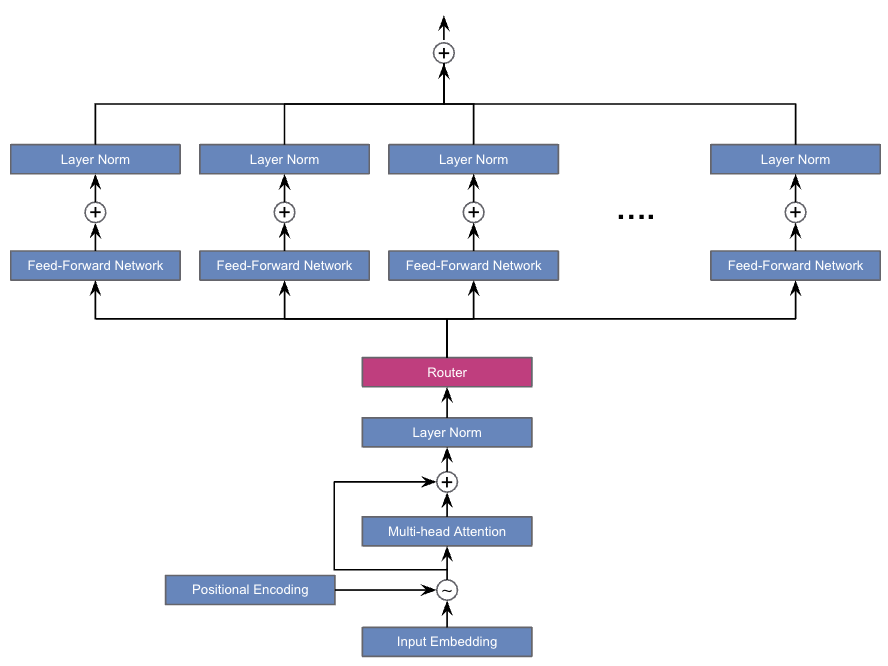
Router Functionality
The router is the cornerstone of Mixtral’s efficiency, functioning as a dynamic selector of experts. At each layer, for every input token, the router chooses two experts to process the token. This is illustrated in Figure 2 where the router sits atop the layer norm and directs inputs to the chosen experts. The selection process is governed by a gating network, represented by the following equation:
\[\sum_{i=0}^{n-1} G(x)_i \cdot E_i(x)\]Here, \(G(x)_i\) is a scalar representing the output of the gating network for the i-th expert, while \(E_i(x)\) is the output of the i-th expert. The gating vector \(G(x)\) is designed to be sparse, meaning most of its elements are zero, and computation is only performed for the non-zero elements, corresponding to the top \(K\) experts with the highest gating values. This sparsity ensures that only the most relevant experts for a given token are engaged.
The gating mechanism is mathematically formalized as:
\[G(x) := \text{Softmax}(\text{TopK}(x \cdot W_g))\]where \(W_g\) is a weight matrix and TopK selects the top \(K\) logits, setting all others to negative infinity, effectively zeroing them out. In Mixtral, \(K\) is set to 2, meaning that for each token, only two experts are actively contributing to the model’s output, hence the designation 8x7B – eight experts per layer in a 7 billion parameter model.
Through this method, Mixtral 8x7B achieves a balance between the expansive capacity of a large parameter set and the practical constraints of inference time and computational resource usage.
Integration of Experts
Within the innovative framework of Mixtral 8x7B, as visualized in Figure 2, the router selects two experts for each token. Once these experts have processed the token independently, their outputs are not left in isolation. Instead, the outputs are combined through an additive process to form the final output for the token. This is mathematically represented as a weighted sum, where the output \(y\) for an input token \(x\) is calculated using the equation:
\[y = \sum_{i=0}^{n-1} \text{Softmax}(\text{Top2}(x \cdot W_g))_i \cdot SwiGLU_i(x)\]Each term in the sum corresponds to one of the two selected experts, with the softmax function ensuring that the gating network’s outputs \(G(x)\) act as weights, conferring the appropriate influence to each expert’s contribution.
Note 1: No details are provided regarding the training dataset.
Note 2: Another distinction between Mixtral 8x7B and the conventional transformer lies in the substitution of the standard FFN with the SwiGLU activation function within its expert layers.
Experiments
The primary aspects of the experimental setups are as follows:
- Tasks: Commonsense Reasoning, World Knowledge, Reading Comprehension, Mathematical Problem-solving, and Code Generation
- Dataset: For commonsense reasoning, datasets such as Hellaswag, Winogrande, and CommonsenseQA were used. World knowledge was tested using the NaturalQuestions and TriviaQA datasets. Reading comprehension abilities were gauged via BoolQ and QuAC. For mathematics and code generation, the GSM8K and Humaneval datasets were instrumental, respectively.
- Baselines: Llama2 70B and GPT-3.5
One interesting finding from the experiments is the apparent randomness in the selection of experts by the router for processing tokens, with no noticeable pattern in expert choice across different inputs. However, their analysis reveals a tendency for consecutive tokens to be processed by the same expert, suggesting a behavior of localized expertise within the model’s architecture.
Conclusion
In conclusion, the Mixtral 8x7B model leverages the potential of integrating Sparse Mixture of Experts (SMoE) within a transformer architecture to enhance efficiency and effectiveness in language processing tasks. Through its innovative router mechanism and SwiGLU activation functions, Mixtral demonstrates superior performance across a range of benchmarks.
Here are some more articles relevant to this one: