Paper Review - Week 36
Here is the list of the most interesting papers published in this week:
Large Language Models as Optimizers
Introduction
In this paper, the authors are using LLMs to solve optimization problems. The fundamental idea is to use optimized prompts as input for the language model, rather than explicitly constructing complex mathematical models or relying on conventional solvers like CPLEX or Gurobi. This inspiring approach simplifies how optimization problems are presented to the model, providing flexibility and reducing the requirement for domain-specific expertise. It also demonstrates that language models can effectively handle diverse optimization problems and may outperform traditional heuristic methods in certain cases.
Research Gap
The advantages of using LLMs for such purpose can be considered as follows:
- By using optimized prompts, the need for creating complex mathematical models or constraints for optimization problems is reduced. This simplifies the way optimization problems are presented to the model.
- Solving complex optimization problems requires expertise in both the problem domain and optimization techniques. Using language models with optimized prompts potentially requires less domain-specific knowledge, making optimization more accessible.
- The authors also demonstrate that LLMs can perform well on various optimization problems, even outperforming traditional heuristic approaches in some cases.
- The optimized prompts found for one problem can sometimes be applied to similar problems, as demonstrated in the transferability experiments.
Generally, the authors demonstrated that using LLMs with optimized prompts is a promising approach for addressing optimization problems, offering simplicity, flexibility, and potential benefits over traditional methods. However, it’s important to note that this approach might not be suitable for all optimization problems and has its own limitations, as mentioned in the research.
Solution: ORPO Framework
The researchers propose a framework named OPRO. In this framework, they create a meta-prompt. The meta-prompt consists of two key components:
- Task Description: This part of the meta-prompt provides a description of the optimization problem to be solved. It typically includes problem-specific details.
- Generated Prompts and Corresponding Accuracy Pairs: This part consists of pairs of generated prompts (candidate instructions) and their corresponding accuracy scores. These prompts are generated by the language model during the optimization process. They represent potential instructions for solving the problem.
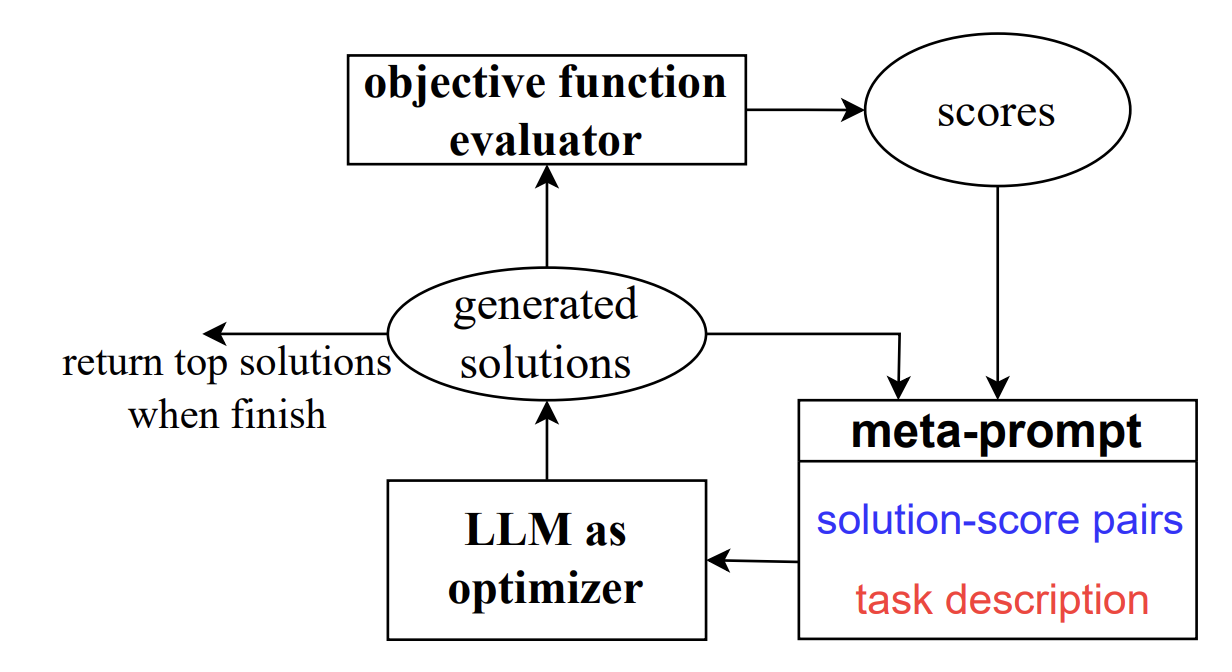
Now, we can review the whole optimization process and its steps; To make the whole process as clear as possible, let us leverage an example. Let us say we have an optimization problem related to scheduling a set of tasks. So, we want to find the most efficient way to assign these tasks to workers while minimizing the overall time taken.
Step 1: The optimization process is initiated by providing the meta-prompt to an LLM. As mentioned earlier the meta-prompt contains two parts: task description and generated prompts and their corresponding accuracy pair. For example, the meta prompt can be:
- Task Description: You need to assign these tasks to workers while minimizing the total time taken. The tasks have different durations and dependencies.
- Pairs of Prompts and Their Accuracy:
- “Minimize time by finding the optimal task assignment.” (Prompt) - 80% accuracy
- “Distribute tasks efficiently to reduce total time.” (Prompt) - 75% accuracy
- “Schedule tasks to minimize the overall duration.” (Prompt) - 85% accuracy
The LLM takes in the entire context, including the task description and the pairs of prompts and accuracy scores. It uses the information in the meta-prompt to generate instructions and attempts to solve the optimization problem. For example, let us assume that the LLM generate the following instruction and solution:
- Instruction: Optimize the task assignment for minimal time.
- Solution: Assign task A to worker 1, task B to worker 2, and task C to worker 3 for the shortest completion time.
Step 2: Now, the generated solution should be evaluated to measure its accuracy. The accuracy of the provided solution is typically measured by comparing it to the known or optimal solution for the given optimization problem. If the problem is a mathematical optimization task, accuracy could be determined by calculating the error or the deviation of the LLM’s solution from the known optimal solution. For example, if the LLM is solving the Traveling Salesman Problem, accuracy could be measured as the percentage difference between the length of the path found by the LLM and the length of the shortest path possible. The smaller the difference, the higher the accuracy. Let us say that, in our example, the accuracy is 87%.
Step 3: The pair of the LLM-generated prompt and its corresponding accuracy score is added to the meta-prompt. In each optimization step, this new information is appended to the existing meta-prompt. So, here, the updated meta-prompt would be:
- Task Description: You need to assign these tasks to workers while minimizing the total time taken. The tasks have different durations and dependencies.
- Pairs of Prompts and Their Accuracy:
- “Minimize time by finding the optimal task assignment.” (Prompt) - 80% accuracy
- “Distribute tasks efficiently to reduce total time.” (Prompt) - 75% accuracy
- “Schedule tasks to minimize the overall duration.” (Prompt) - 85% accuracy
- “Optimize the task assignment for minimal time.” (Prompt) - 87% accuracy
Step 4: Now, the updated meta-prompt is used to repeat steps 2 and 3. This process continues until one of the following conditions is met:
- The LLM’s generated solutions reach a satisfactory level of accuracy, and further optimization does not significantly improve the results
- A predefined maximum number of optimization steps is reached.
Experiments
The authors focus on two optimization problems for their experiments:
- Prompt Optimization for Natural Language Tasks: This part focuses on optimizing prompts for natural language tasks. They conduct experiments on datasets such as GSM8K (grade school math word problems) and Big-Bench Hard (BBH), which consists of various challenging tasks. The primary objective is to optimize prompts for these datasets to maximize task accuracy. The OPRO framework was quite successful in optimizing prompts for various natural language tasks. Instructions generated through prompt optimization improved task accuracy significantly compared to initial or baseline prompts. The instructions generated by OPRO demonstrated high transferability and outperformed baseline prompts on different datasets within the same domain.
- Traveling Salesman Problem (TSP): The researchers also apply their framework, OPRO, to the Traveling Salesman Problem, a classic combinatorial optimization problem. They evaluate the performance of OPRO in comparison to heuristic algorithms and measure the optimality gap. The OPRO framework, when applied to the TSP, demonstrated promising results on smaller-scale TSP problems. However, its performance on larger-scale TSP problems degraded, with heuristics outperforming the language models.
Conclusion
This paper presents an innovative approach that leverages Large Language Models (LLMs) to address optimization problems through prompt optimization. The OPRO framework simplifies the presentation of optimization tasks to LLMs, potentially reducing the need for domain-specific expertise and outperforming traditional heuristics in specific cases. The experiments conducted on natural language tasks demonstrate OPRO’s success in improving task accuracy and transferability, while its performance in solving the Traveling Salesman Problem (TSP) varies, excelling in smaller-scale instances but being outperformed by heuristics in larger-scale problems. This approach showcases the promise of LLMs in optimization but is subject to domain-specific constraints and varying levels of effectiveness.
Here are some more articles relevant to this one: